New library: FlexPhpRouter
I’ve created this router library because none of the available ones fit my taste. Check it out at: https://github.com/bolner/FlexPhpRouter Its packagist.org page: https://packagist.org/packages/tbolner/flex-php-router
Barcarola veneziana no. 4
Aldo Bova is not just a great recorder player, but also an inspiring composer from Italy (currently living in Germany if I know correctly). This piece from him is one of my favourites, therefore I spent some time to record it using a sampled choir voice.
A faster way to calculate logarithm on the soroban
We will discuss a fast way to calculate logarithms on the Japanese abacus (soroban) up to the accuracy of 4 decimal places, without using logarithm tables. The method used here to produce an efficient algorithm for logarithm calculation can be applied to many other complicated functions.
CRTerm – terminal emulator library
My new project, a terminal emulator library which mimics an old CRT display, has finally reached a usable state. See it on its GitHub page: https://github.com/bolner/CRTerm I’ve uploaded a demo to Youtube:
How to convert a PDF from archive.org for tablet
Archive.org is a great website full of book rarities available for free download. The only problem is that most of their PDF files are quiet unreadable, not just on a tablet, but even on a stronger desktop PC, because they are optimized for minimal size, and it can take around 5-10 seconds for a tablet to render a page. This post shows a method for converting those PDF files to larger files (around 4x), which can be comfortably browsed offline even on a tablet.
CozyCL: a comfortable OpenCL library
CozyCL is a very simple, minimalist OpenCL library. You can run programs on your graphics card pretty easily with it, without the need to know anything about the data types of the base libraries (at least for the host program). When I started to learn about GPU programming in the previous weeks, I found even the most handy C++ bindings pretty time-consuming for a beginner, who is mostly interested in getting positive feedback and sense of achievement after a couple of initial attempts.
Multi-threaded Buddhabrot fractal rendering in C++ for 16 bit/channel post-processing
I’ve written the major part of this Buddhabrot rendering program in last August, and after a six months break I carried on with it again this weekend to close the project finally. But before going into details, let`s see what it does:
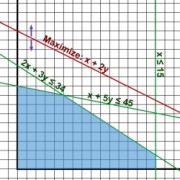
An easy-to-use Simplex solver class
Few days ago I decided to create a C++ implementation of the Simplex algorithm, which is a tool for solving Linear Programming problems. One of my motivations could have been my recent encounter with the Eigen linear algebra library, which really surprised me with its beautiful syntax and easy usage. So I wanted to gain a little experience with Eigen, although some factorization-related project might have suited this purpose better. Another motivational factor was a not yet published project of mine, which might get finished in 1 or 2 months, and would give LP a real application.
A picture of the Moon
This picture of the Moon is made from the average (mean) of 16 RAW images (14 bit), taken on the 30th of May 2012, around 23:30 (UTC+1), at Frankfurt am Main. I used my 9.25 inch Celestron telescope, with an adapter, which reduces its focal length, so the whole Moon fits in the screen, and also produces higher brightness level. The settings for the DSLR camera are: ISO: 100, Shutter speed: 1/400.
Music composition exercise
I’ve just finished this short choral music, made as an exercise for chord progression and voice leading in four sections: soprano, alto, tenor, bass.