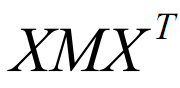Category: Mathematics RSS feed for this category
A faster way to calculate logarithm on the soroban
We will discuss a fast way to calculate logarithms on the Japanese abacus (soroban) up to the accuracy of 4 decimal places, without using logarithm tables. The method used here to produce an efficient algorithm for logarithm calculation can be applied to many other complicated functions.
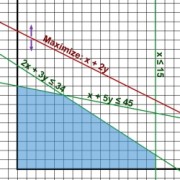
An easy-to-use Simplex solver class
Few days ago I decided to create a C++ implementation of the Simplex algorithm, which is a tool for solving Linear Programming problems. One of my motivations could have been my recent encounter with the Eigen linear algebra library, which really surprised me with its beautiful syntax and easy usage. So I wanted to gain a little experience with Eigen, although some factorization-related project might have suited this purpose better. Another motivational factor was a not yet published project of mine, which might get finished in 1 or 2 months, and would give LP a real application.
Algebraic formulas and matrix symmetry
This post features two examples of algebraic manipulation and their relation to the symmetry of the matrices representing the expressions. The algebraic expressions we investigate are quadratic, multivariate and can be written in the matrix form:
Graph editor and Matrix generator
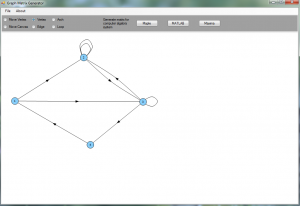
Making matrix representations of graphs always takes a lot of time. For practicing algebraic or spectral graph theory on computer algebra systems, one has to create a lot of graphs. A handy tool can make this easy, which allows to draw graphs and generate code e.g. for Maple with one click. Well I couldn’t find a tool like that, so I made one on the weekend in C#. With it, you can draw custom graphs, including: arbitrary loops, parallel edges, directed edges, etc. and can generate code for these computer algebra systems: Maple, MATLAB, Maxima. Then the code can be
Deadlocks and graph theory
When accessing a database through a series of transactions, a deadlock can occur any time. They are natural companions of transactions. We can decrease their likelihood by rigorously accessing the records and the tables always in the same order, but over a level of complexity we can never be 100% free of them. This is a fair price for the ACID properties. Deadlocks occur very rarely, and when this happens, the only thing to do is to repeat the transaction in the process which had been interrupted by the deadlock detection demon of the database. This is very small performance
An interesting proof of Turán’s theorem
In the past few days I have been reading a nice book about graph theory, including solving the exercises in it. Once I encountered an exercise which I couldn’t solve, so made a little research, and found that the solution is the proof of the Turán’s theorem. The usual proof for this theorem is built on induction, but later I have found a proof which is using a basic inequality. I am sure that I’m not the first one who have seen this solution, although I couldn’t find it on the net yet.
